Facciamo un passo ulteriore lungo il percorso di conoscenza della Psicologia della Complessità. Uno strumento che occupa un posto centrale è quello che abbiamo chiamato Modello di Klein-Wolfram-Langton.
Questo modello si basa sulle Classi di Wolfram-Langton, di cui parleremo oggi.
Come suggerisce il nome, le Classi di Wolfram-Langton sono un sistema di classificazione. Questo sistema viene usato per classificare l’evoluzione dei sistemi dinamici nel loro ambiente. Sembra infatti che esistano solo quattro “tipi” di evoluzione possibili e questi quattro tipi sono appunto le quattro Classi di Wolfram-Langton.
Il modo migliore per prendere confidenza con questi concetti è quello di ripercorrere il cammino compiuto dagli studiosi per arrivare alla loro formulazione.
Prima di tutto va posta la domanda: che cosa si intende per sistema dinamico? Chiamiamo così qualsiasi sistema si componga di due parti: stato (condizione del sistema a un certo istante) e dinamica (insieme di regole che stabiliscono come cambia lo stato nel tempo).
Una volta definito l’oggetto di studio, il passo successivo è quello di individuare le variabili di stato del sistema dinamico. Le variabili di stato sono le caratteristiche misurabili del sistema che, istante per istante, definiscono in modo esauriente e univoco la condizione del sistema stesso. In altre parole: in un certo istante, conoscere il valore di tutte le variabili di stato permette di conoscere lo stato del sistema dinamico in quel preciso momento. Man mano che il sistema dinamico modifica la propria condizione, cambia il valore delle variabili di stato. Dunque il cambiamento nel tempo delle variabili di stato corrisponde puntualmente all’evoluzione del sistema.
Se quello che ci interessa è come evolve il sistema, allora molte sue caratteristiche possono essere trascurate. Supponiamo che ci interessi studiare come un libro cade sul pavimento. In questo caso il sistema dinamico è il libro e la sua evoluzione è la caduta sul pavimento. Quali sono le variabili di stato che ci interessano? In questo caso potrebbe bastarne una sola: la distanza del libro dal pavimento. Di quale libro si tratti, infatti, è irrilevante rispetto alla sua evoluzione. Il numero di pagine, l’autore, l’argomento trattato, l’immagine in copertina, se lo giudichiamo un libro interessante oppure no, se lo abbiamo comprato o preso in prestito, sono tutte caratteristiche che in determinate circostanze potrebbero avere una notevole importanza, ma non se studiamo la caduta del libro sul pavimento. Come evolve il sistema “libro che cade”? Per rispondere, basta osservare come cambiano nel tempo le variabili di stato. In questo caso, l’unica variabile in gioco ha come valore iniziale l’altezza da cui il libro cade, poi il suo valore decresce sempre più rapidamente fino a zero. Quando la variabile di stato raggiunge lo zero, il sistema non evolve più: diremo allora che ha raggiunto uno stato stabile. Il valore zero si è comportato come una calamita per la variabile di stato: l’ha “attirata” a sé e non l’ha più lasciata andare. Per questo motivo, in questo modello, il valore zero è chiamato attrattore.
Quando per descrivere l’evoluzione di un sistema dinamico occorrono due variabili di stato, possiamo costruire uno spazio a due dimensioni, ovvero un piano cartesiano, nel quale a ogni punto corrisponde in modo univoco un preciso valore per ciascuna delle due variabili di stato. Il piano cartesiano così costruito viene chiamato spazio degli stati.
Nel caso in cui le variabili di stato siano tre, lo spazio degli stati diventa uno spazio euclideo tridimensionale. Anche in questo caso, a ogni punto dello spazio corrisponde un preciso valore per ciascuna delle tre variabili di stato.
Quando le variabili di stato sono più di tre, non è più possibile visualizzare lo spazio degli stati: lo si può solo immaginare. Dobbiamo immaginare lo spazio degli stati come un iperspazio pluridimensionale in cui ciascuna dimensione (ciascun asse cartesiano) misura il valore di una variabile di stato.
Per esempio, come potrebbe essere lo spazio degli stati di una partita a scacchi? Una possibilità potrebbe essere quella di immaginare un asse cartesiano per ciascuna delle 64 caselle della scacchiera. In pratica, in questo caso, le variabili di stato rappresentano la condizione di ogni casella. In ogni istante, ciascuna variabile di stato può assumere uno solo tra i seguenti “valori”: vuota, pedone bianco, pedone nero, re bianco, re nero, regina bianca, regina nera, alfiere bianco, alfiere nero, cavallo bianco, cavallo nero, torre bianca e torre nera. In ogni istante della partita, la disposizione dei vari pezzi sulla scacchiera corrisponde in modo univoco a un punto nell’iperspazio a 64 dimensioni che nasce incrociando i 64 assi cartesiani corrispondenti alle caselle del tavoliere. Dopo ogni mossa, questo punto nell’iperspazio degli stati si sposta, disegnando una traiettoria. A ogni partita corrisponde una e una sola traiettoria nell’iperspazio degli stati.
In una partita a scacchi, l’evoluzione del sistema è governata dalle regole del gioco e dalle strategie dei due giocatori. Data una certa configurazione, la configurazione all’istante successivo è determinata dalla mossa decisa del giocatore a cui spetta muovere, che però può scegliere solo nell’ambito delle mosse lecite stabilite dalle regole. In altre parole, quando la traiettoria disegnata dalla partita tocca un certo punto nell’iperspazio degli stati, non può procedere liberamente verso qualsiasi altro punto. Può proseguire raggiungendo solo alcuni punti e non altri. Si noti che, nonostante questo limite, il numero delle partite/traiettorie possibili rimane spaventosamente grande. Se limitiamo la nostra attenzione alle prime 10 mosse della partita, 5 del giocatore bianco e 5 del nero, il numero totale di traiettorie possibili è poco meno di 70 mila miliardi. Quante sono le traiettorie possibili in assoluto? Nessuno è mai riuscito a dare una risposta a questa domanda. Il “padre” della teoria dell’informazione, Claude Shannon, nel 1950 stimò che questo numero potrebbe aggirarsi su 10 elevato a 120, ovvero un “1” seguito da 120 zeri. Per renderci conto di quanto sia grande questo numero, basti pensare che gli scienziati stimano che il numero di particelle nell’intero universo sia “solo” 10 elevato a 80 (1 seguito da 80 zeri).
Anche se il calcolo delle traiettorie possibili ha un suo fascino, in realtà non ha nulla a che fare con le Classi di Wolfram-Langton. La domanda più pertinente, infatti, non è quante siano le traiettorie possibili per un dato sistema dinamico; è invece: cosa fanno queste traiettorie nel loro spazio degli stati?
Studiando le traiettorie disegnate nello spazio degli stati dall’evoluzione dei sistemi dinamici, ci si accorge che ci sono alcuni “comportamenti” tipici e ricorrenti. Vediamone alcuni aiutandoci con degli esempi.
Consideriamo un ecosistema formato da due popolazioni che condividono la stessa nicchia ecologica e che interagiscono tra loro. La prima popolazione è costituita da predatori, per esempio linci, che si nutrono degli individui della seconda popolazione, cioè le prede, che nel nostro esempio potrebbero essere lepri. Quando ci sono poche linci in circolazione, le lepri prosperano e si moltiplicano. Man mano che le prede aumentano, le linci hanno a disposizione più cibo, per cui si moltiplicano a loro volta. Quando però i predatori diventano tanti, le prede vengono decimate e cominciano a scarseggiare. Questo causa la morte per mancanza di cibo delle linci, che diminuiscono di numero. Dopodiché il ciclo si ripete. Come potremmo rappresentare questo sistema? Bastano due variabili di stato: la popolosità di prede e predatori. Rappresentando graficamente l’evoluzione di questo sistema, quello che si vede è che la traiettoria è un ciclo chiuso:
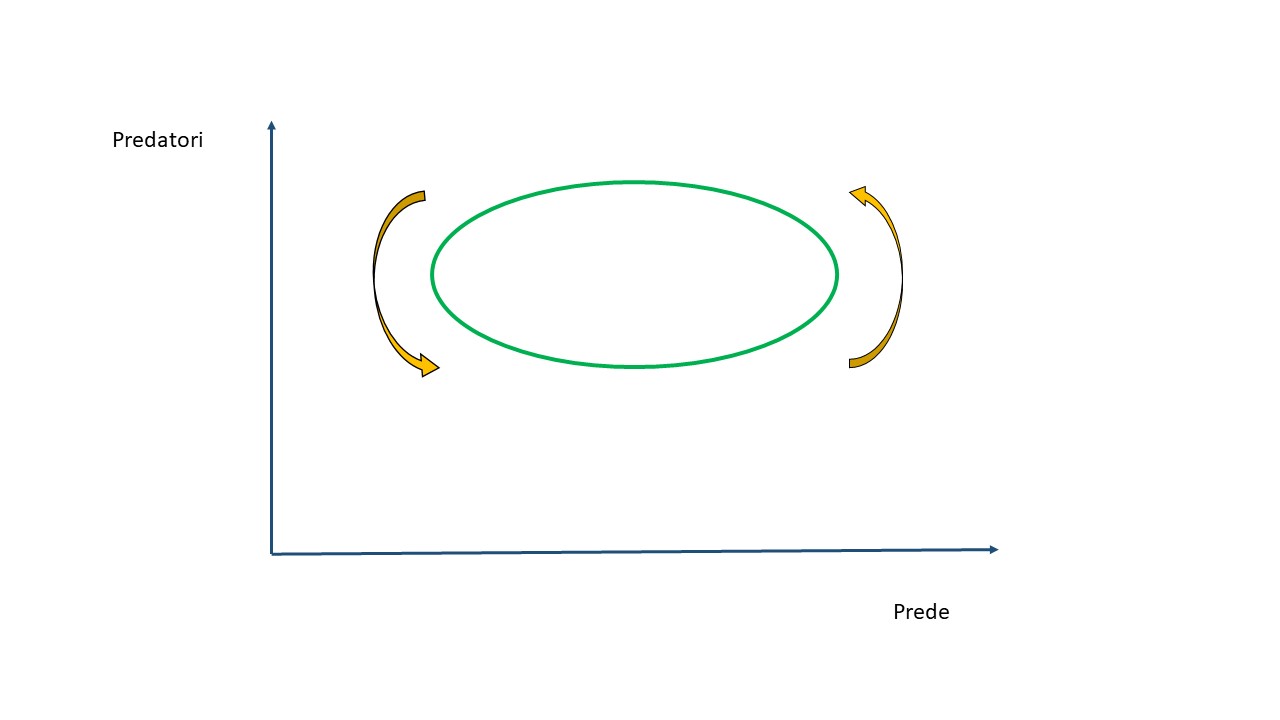In casi come questo, in cui la traiettoria è ciclica, si può affermare che l’attrattore nello spazio degli stati sia l’orbita a cui la traiettoria tende e sulla quale si stabilizza.
Facciamo un altro esempio. Consideriamo un pendolo che oscilla. Le variabili di stato sono l’angolo formato dal pendolo rispetto alla verticale e la velocità di oscillazione. Quando il pendolo oscilla a destra della verticale, l’angolo è positivo, quando oscilla a sinistra, l’angolo è negativo. Quando oscilla in senso antiorario, la velocità è positiva; in senso orario, la velocità è negativa. Spostando il pendolo dalla sua posizione di equilibrio, diciamo verso destra, l’angolo iniziale è positivo e la velocità è nulla. Lasciando andare il pendolo, l’angolo diminuisce fino a zero e la velocità aumenta in valore assoluto; poiché il pendolo sta oscillando in senso orario, la velocità è negativa. Quando l’angolo è zero, la velocità è al suo massimo (negativo). Dopodiché l’angolo diventa negativo e la velocità diminuisce in valore assoluto fino a zero. A questo punto il pendolo torna indietro: l’angolo negativo tende allo zero e la velocità, che questa volta è positiva, aumenta in valore assoluto fino al suo massimo, dopodiché sia l’angolo che la velocità diventano positivi: l’angolo tende al valore iniziale (senza raggiungerlo) e la velocità decresce fino a zero. A questo punto l’intera oscillazione si ripete, ma a causa dell’attrito i valori assoluti dell’angolo e della velocità diminuiscono progressivamente man mano che il pendolo oscilla.
In questo caso la traiettoria disegnata è una spirale:
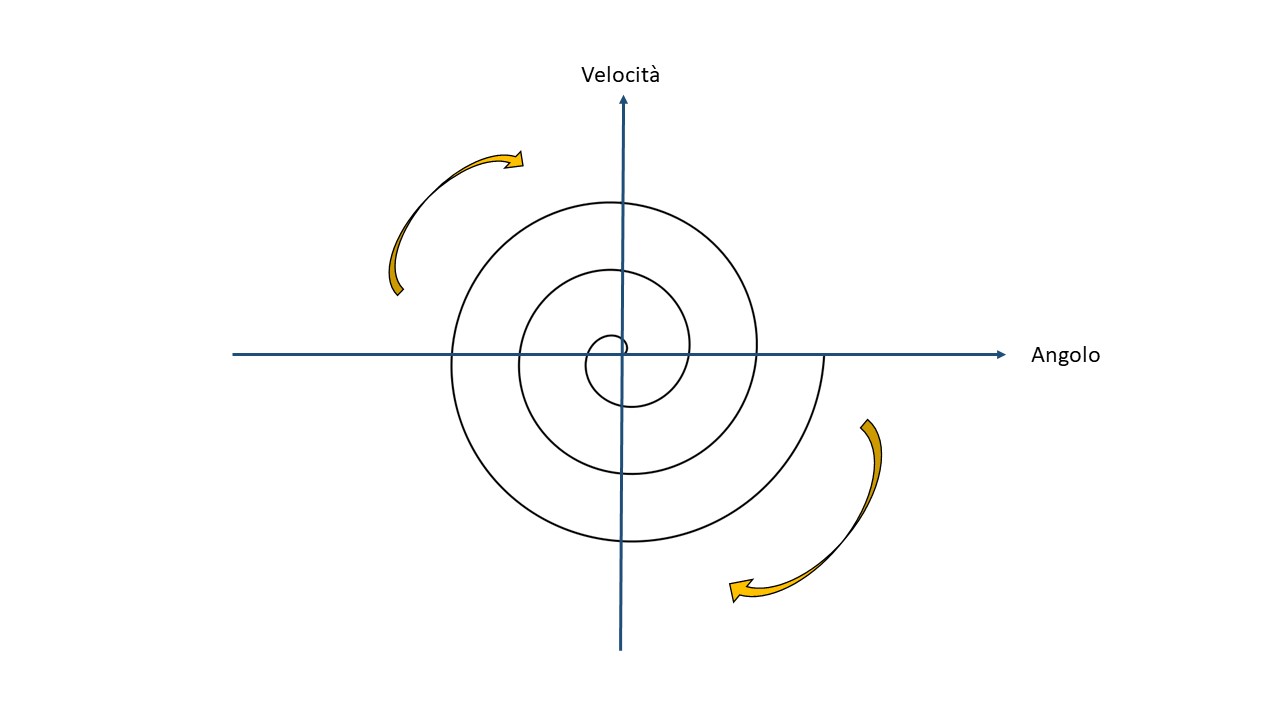L’attrattore nello spazio degli stati del pendolo è lo stato stabile (0, 0) in cui angolo e velocità sono nulli.
Consideriamo ora un sistema dinamico molto studiato dai meteorologi: una massa d’aria, ad esempio una nuvola. Nel 1963 il meteorologo Edward Lorenz costruì un modello in cui tale sistema era rappresentato dalle variabili di stato x, y e z. Nel modello di Lorenz, x era proporzionale alla velocità del fluido; y era proporzionale alla differenza di temperatura tra gli elementi di fluido in moto ascendente e discendente; z era inversamente proporzionale alla linearità del profilo verticale della temperatura (il profilo verticale della temperatura è la variazione di temperatura rispetto alla quota).
La traiettoria che rappresenta l’evoluzione nel tempo di questo sistema ha una forma molto particolare – e molto famosa:
In questo caso, l’attrattore non è né un punto, né un’orbita; è un’intera porzione dello spazio degli stati. Quest’area tridimensionale, nota come attrattore di Lorenz, ha una forma molto strana, sembra una farfalla. Essendo appunto strani, gli attrattori di questo tipo sono noti come attrattori strani.
Nella prima metà degli anni Ottanta, il fisico Stephen Wolfram, studiando le traiettorie dei sistemi dinamici noti come automi cellulari, arrivò alla conclusione che tutte le evoluzioni possibili di tali sistemi rientrano in una delle seguenti classi:
Classe I: qualsiasi sia lo stato iniziale, il sistema evolve verso uno stato stabile. Nello spazio degli stati, la traiettoria si dirige verso un attrattore puntiforme e lì si ferma. Come accade con il pendolo.
Classe II: il sistema evolve in modo ciclico. Nello spazio degli stati, la traiettoria viene attratta da un’orbita da cui non si allontana più. È il caso dell’ecosistema formato da prede e predatori.
Classe III: è il caso in cui il sistema manifesta un comportamento irregolare, caotico. Nello spazio degli stati non c’è alcun attrattore.
Classe IV: il sistema manifesta comportamenti sofisticati e affascinanti. Nello spazio degli stati ci sono attrattori strani. Come nel modello di Lorenz.
Anche se gli esempi che abbiamo fatto riguardano sistemi dinamici diversi dagli automi cellulari, quando Wolfram enunciò la sua classificazione, non pensava affatto che potesse essere estesa ad altri sistemi. Addirittura Wolfram era convinto che i comportamenti della Classe IV fossero una peculiarità esclusiva degli automi cellulari.
Fine prima parte